Ejercicio 1
Se descarga el fichero de la url indicada:
Se lee o importa el contenido del fichero en R:
'data.frame': 6259 obs. of 10 variables:
$ precio : num 1499 1795 1595 1849 3295 ...
$ velocidad : num 25 33 25 25 33 66 25 50 50 50 ...
$ hd : num 80 85 170 170 340 340 170 85 210 210 ...
$ ram : num 4 2 4 8 16 16 4 2 8 4 ...
$ pantalla : num 14 14 15 14 14 14 14 14 14 15 ...
$ cd : chr "no" "no" "no" "no" ...
$ multi : chr "no" "no" "no" "no" ...
$ buenfabricante: chr "si" "si" "si" "no" ...
$ numprecios : num 94 94 94 94 94 94 94 94 94 94 ...
$ numes.ene1993 : num 1 1 1 1 1 1 1 1 1 1 ...Se realiza un resumen descriptivo de los datos:
precio velocidad hd ram
Min. : 949 Min. : 25.00 Min. : 80.0 Min. : 2.000
1st Qu.:1794 1st Qu.: 33.00 1st Qu.: 214.0 1st Qu.: 4.000
Median :2144 Median : 50.00 Median : 340.0 Median : 8.000
Mean :2220 Mean : 52.01 Mean : 416.6 Mean : 8.287
3rd Qu.:2595 3rd Qu.: 66.00 3rd Qu.: 528.0 3rd Qu.: 8.000
Max. :5399 Max. :100.00 Max. :2100.0 Max. :32.000
pantalla cd multi buenfabricante
Min. :14.00 Length:6259 Length:6259 Length:6259
1st Qu.:14.00 Class :character Class :character Class :character
Median :14.00 Mode :character Mode :character Mode :character
Mean :14.61
3rd Qu.:15.00
Max. :17.00
numprecios numes.ene1993
Min. : 39.0 Min. : 1.00
1st Qu.:162.5 1st Qu.:10.00
Median :246.0 Median :16.00
Mean :221.3 Mean :15.93
3rd Qu.:275.0 3rd Qu.:21.50
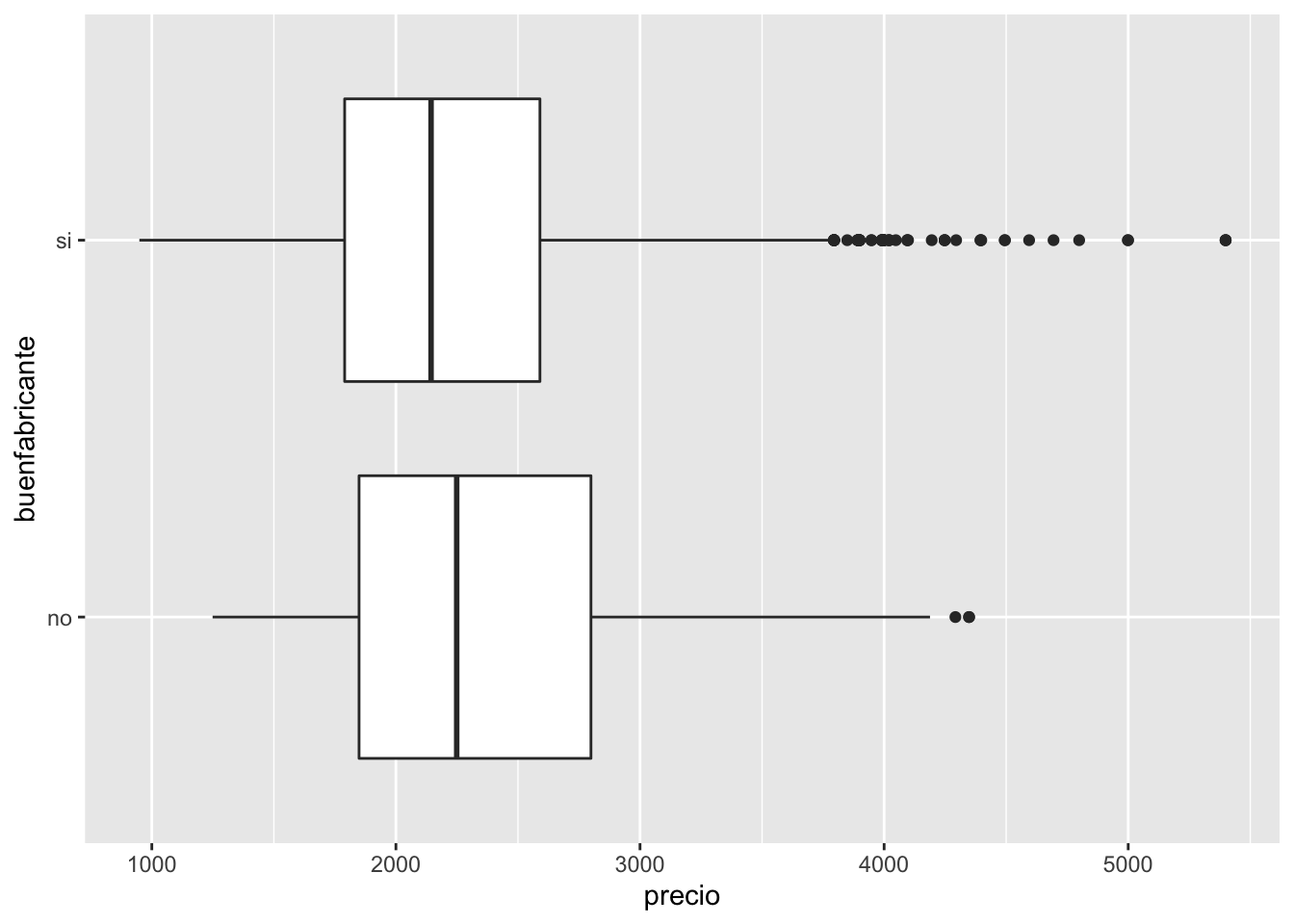
Max. :339.0 Max. :35.00 Se construye un gráfico con ggplot2
Ejercicio 2
Creamos una matriz \(3 \times 3\) con elementos aleatorios:
[,1] [,2] [,3]
[1,] -0.6264538 1.5952808 0.4874291
[2,] 0.1836433 0.3295078 0.7383247
[3,] -0.8356286 -0.8204684 0.5757814Se calculan las máximos, mínimos y medias por columnas de esta matriz.
Procedimiento 1:
[1] 0.1836433 1.5952808 0.7383247[1] -0.8356286 -0.8204684 0.4874291[1] -0.4261464 0.3681067 0.6005117Procedimiento 2:
[1] 0.1836433 1.5952808 0.7383247[1] -0.8356286 -0.8204684 0.4874291[1] -0.4261464 0.3681067 0.6005117Procedimiento 3:
Procedimiento 4:
Utilizando la filosofía “tidyverse”:
# A tibble: 3 × 3
V1 V2 V3
<dbl> <dbl> <dbl>
1 -0.626 1.60 0.487
2 0.184 0.330 0.738
3 -0.836 -0.820 0.576Ejercicio 3
La función se puede construir usando lo visto en el ejercicio 2:
Un ejemplo de uso:
$Maximos
[1] 0.1836433 1.5952808 0.7383247
$Minimos
[1] -0.8356286 -0.8204684 0.4874291
$Medias
[1] -0.4261464 0.3681067 0.6005117Escribir la función en un fichero aparte e incorporarla en un documento R Markdown…